TypeScript刷LeetCode[6] 剑指 Offer 10- I. 斐波那契数列

题目

难度：简单

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：

F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.

斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

示例 1：

输入：n = 2
输出：1

示例 2：

输入：n = 5
输出：5

代码

暴力递归（不可取）

LeetCode 上 n=44 时就会超时

function fib(n: number): number {
    switch (n) {
        case 0:
            return 0
        case 1:
            return 1
        case 2:
            return 1
        default:
            return fib(n - 1) + fib(n - 2)
    }
}

带缓存的递归

这道题有该死的取模，不然代码还是很好看懂的

function fib(n: number): number {
    return solve(n) % (1e9 + 7)
}

function solve(n: number): number {
    if (cache[n] === undefined) {
        cache[n] = fib(n - 1) + fib(n - 2)
    }
    return cache[n]
}

let cache = [0, 1, 1]

动态规划

动态规划用到的状态转移方程：

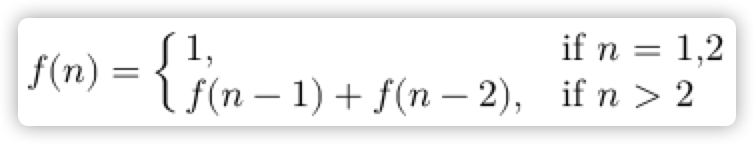
将上一个方法里的 cache 直接初始化为长度为 n+1 的数组，取下标对应的值为当前 fib(n)的值，再利用循环去解决所有数字直到得出结果

占用 O(n)的时间和 O(n)的空间

function fib(n: number): number {
    if (n === 0) {
        return 0
    }
    if (n === 1) {
        return 1
    }
    let dp = Array(n + 1).fill(0)
    dp[1] = dp[2] = 1
    for (let i = 3; i <= n; i++) {
        dp[i] = (dp[i - 1] % (1e9 + 7)) + (dp[i - 2] % (1e9 + 7))
    }
    return dp[n] % (1e9 + 7)
}

动态规划（优化）

注意到上一个方法里，对结果而言，dp 数组只取最后一位，前面的空间可以在循环时舍弃，所以理论上只需要 O(n)的时间和 O(1)的空间

用两个变量 prev 和 curr 表示前一个数字和当前数字，不断加和得出结果

function fib(n: number): number {
    if (n === 0) {
        return 0
    }
    if (n === 1 || n === 2) {
        return 1
    }
    let prev = 1,
        curr = 1
    for (let i = 3; i <= n; i++) {
        let sum = prev + curr
        prev = curr
        curr = sum % (1e9 + 7)
    }
    return curr
}

点击刷本题吊打我 (opens new window)